2021年7月第三周
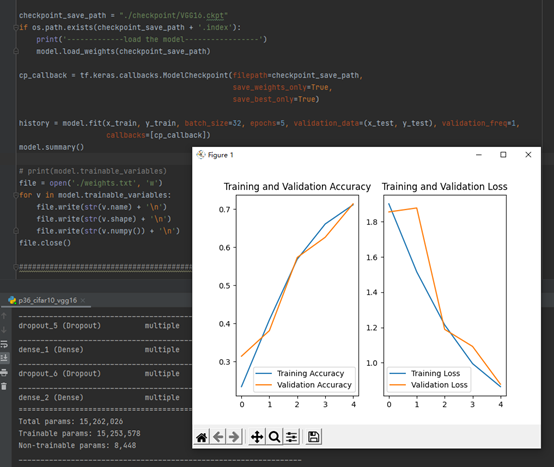
1.编写卷积神经网络程序,实现五种花朵分类
数据:
训练: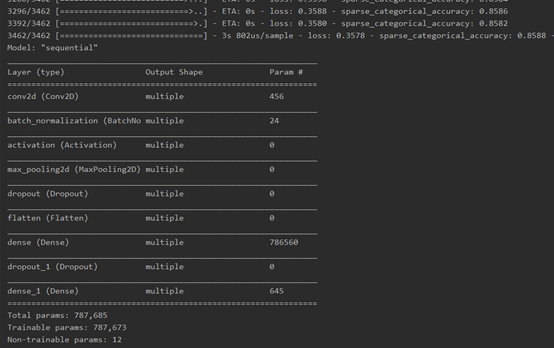
测试: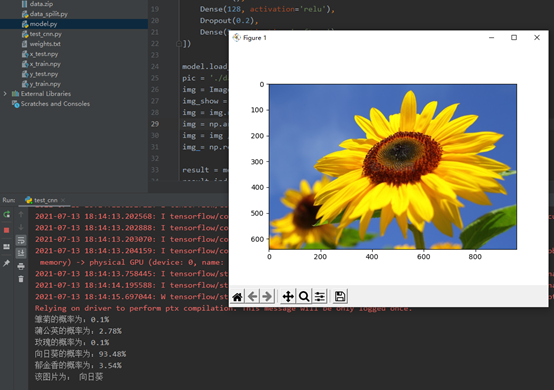
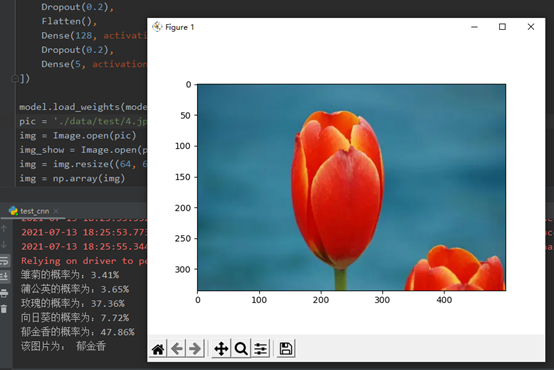
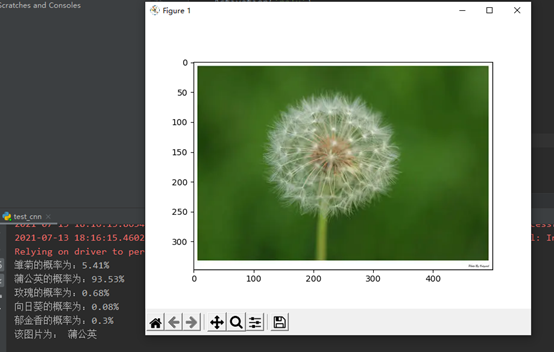
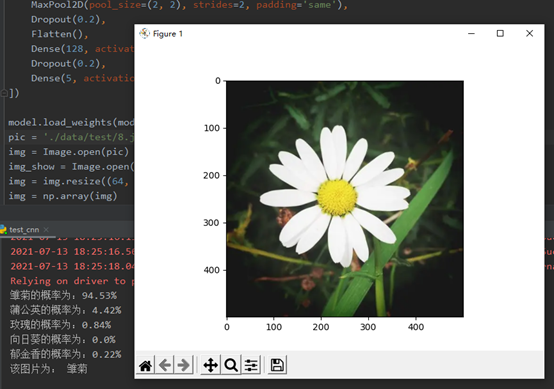

2.学习了【北京大学】Tensorflow2.0教程
循环神经网络具有记忆性、参数共享并且图灵完备(Turing completeness),因此在对序列的非线性特征进行学习时具有一定优势^ [4]^[ ]() 。循环神经网络在自然语言处理(Natural Language Processing, NLP),例如语音识别、语言建模、机器翻译等领域有应用,也被用于各类时间序列预报。引入了卷积神经网络(Convolutional Neural Network,CNN)构筑的循环神经网络可以处理包含序列输入的计算机视觉问题。
循环核:参数时间共享,循环层提取时间信息。
循环神经网络:借助循环核提取时间特征后,送入全连接网络。
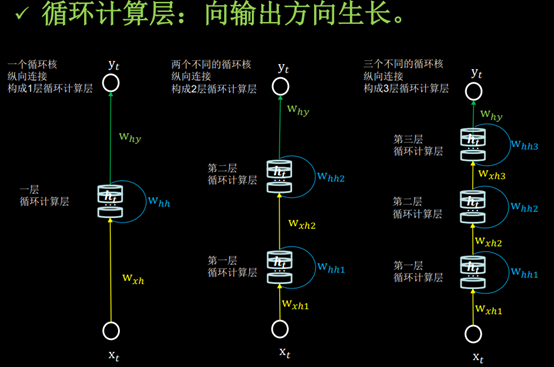

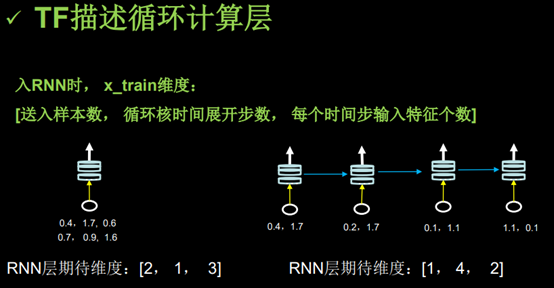
例子:(1)循环网络计算过程-字母预测
独热码,在英文文献中称做 one-hot code, 直观来说就是有多少个状态就有多少比特,而且只有一个比特为1,其他全为0的一种码制。通常,在通信网络协议栈中,使用八位或者十六位状态的独热码,且系统占用其中一个状态码,余下的可以供用户使用。
例如,有6个状态的独热码状态编码为:000001,000010,000100,001000,010000,100000。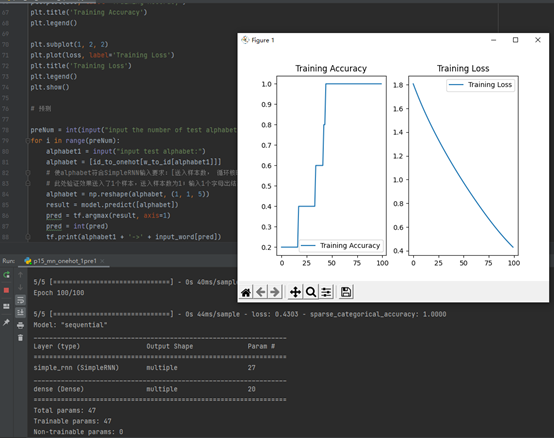
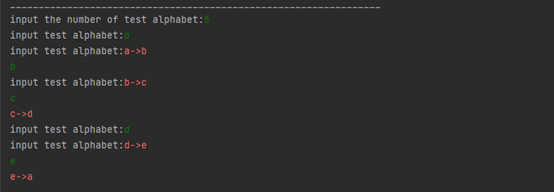
(2)用RNN实现输入一个字母,预测下一个字母 (One hot 编码)
输入abcd输出e
输入bcde输出a
输入cdea输出b
输入deab输出c
输入eabc输出d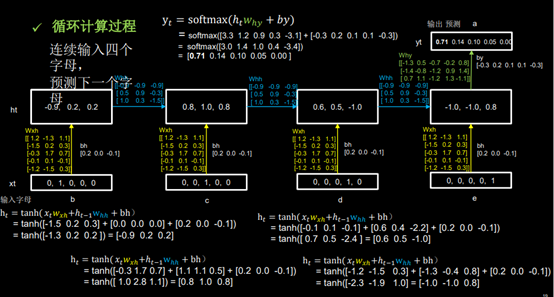
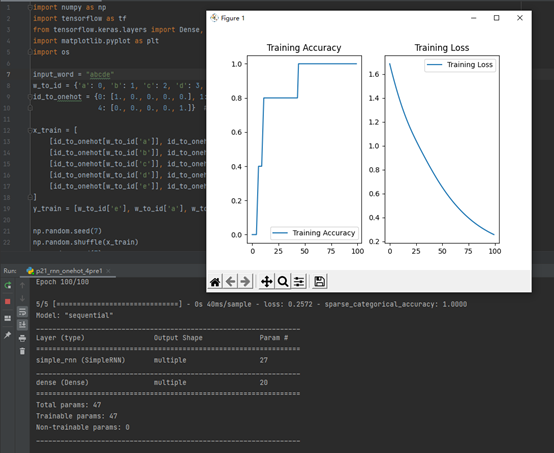

(3)RNN实现股票预测

(4)用LSTM实现股票预测
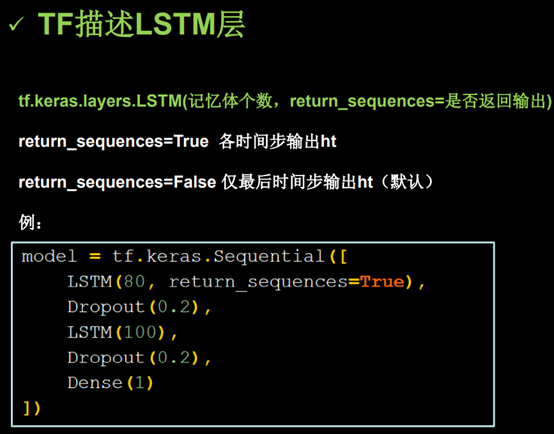

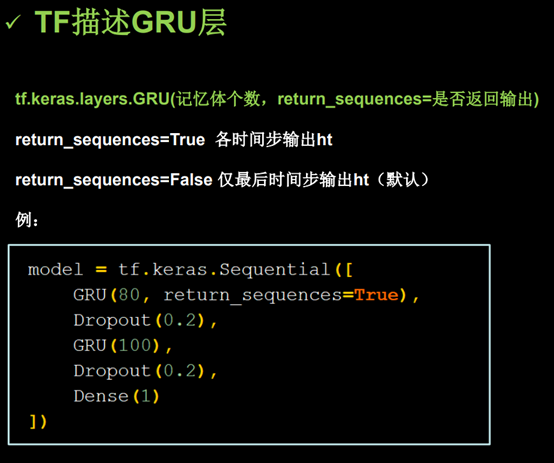
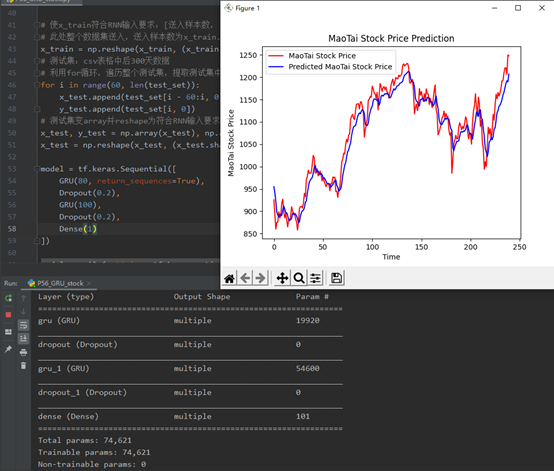
(5)用GRU实现股票预测
遇到的问题和解决办法
Tensorflow与numpy版本不匹配。
解决:对应https://docs.floydhub.com/guides/environments/ 降低numpy版本
2021年7月第二周
1.安装CUDA和cuDNN使用gpu加速
https://blog.csdn.net/wbing96/article/details/108914071
https://blog.csdn.net/sinat_23619409/article/details/84202651


GPU性能太差提示显存不够,可通过减少batch_size解决。
2.学习了【北京大学】Tensorflow2.0教程
卷积:
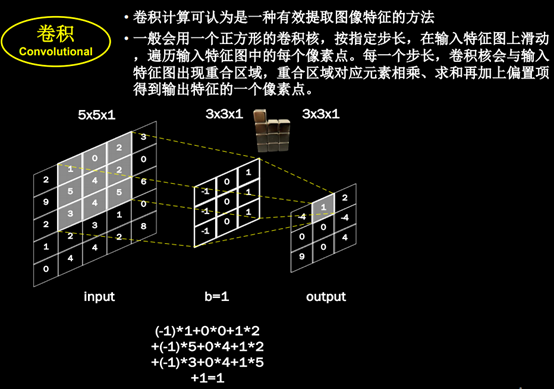

感受野:(Receptive Field)卷积神经网络各输出特征图中的每个像素点,在原始输入图片上映射区域的大小。
全零填充:卷积计算保持输入特征图的尺寸不变,在输入特征图周围填充0

批标准化:(Batch Normalization, BN) 标准化:使数据符合0均值,1为标准差的分布。批标准化:对一小批数据(batch),做标准化处理。常用在卷积操作和激活操作之间。
池化:用于减少特征数据量,最大池化可提取图片纹理,均值池化可保留背景特征。
舍弃:(Dropout)在神经网络训练时,将一部分神经元按照一定比例从神经网络中暂时舍弃,神经网络使用时,被舍弃的神经元恢复链接。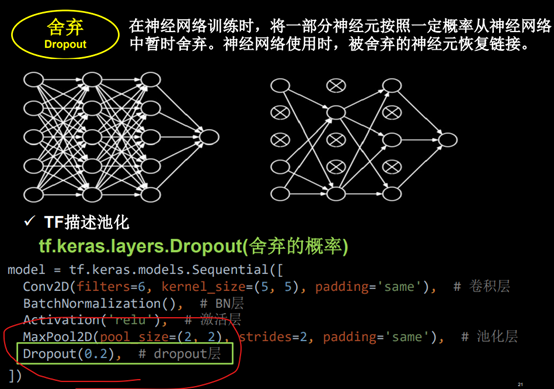
卷积神经网络:借助卷积核提取特征后,送入全连接网络。
卷积-特征提取器-CBAPD即Conv2D(卷积层)、BN层、Activation(激活层)、MaxPool2D(池化层)、Dropout
Cifar10数据集: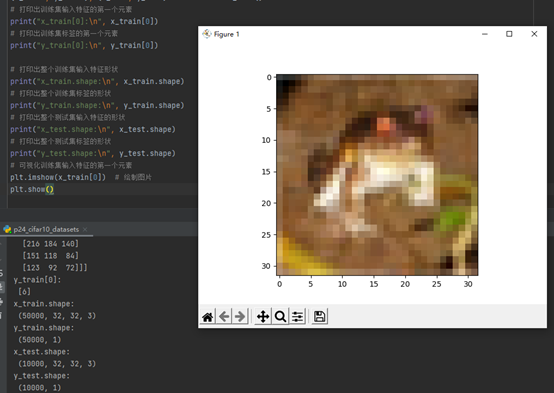
卷积神经网络搭建: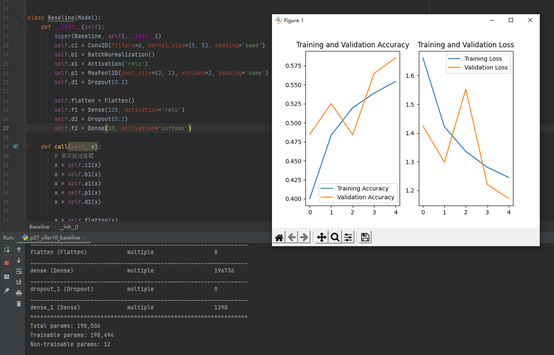

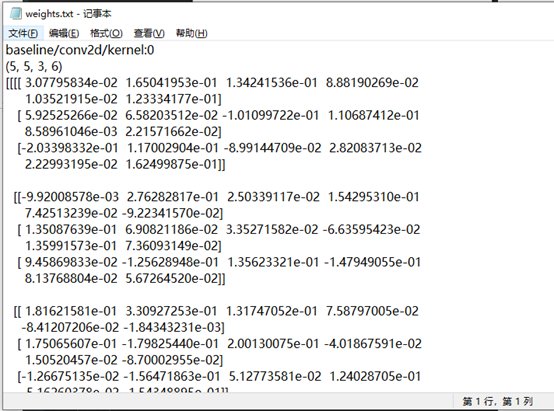
五个经典卷积神经网络
LeNet、AlexNet、VGGNet、InceptionNet、ResNet
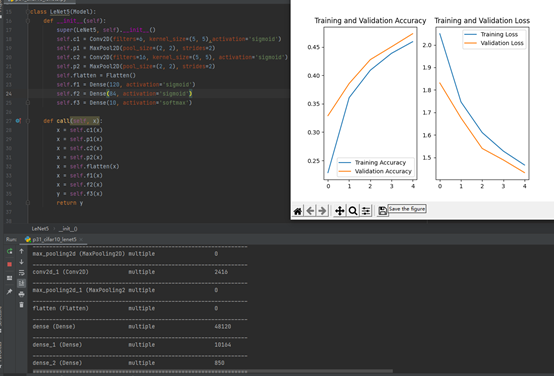
1.LeNet
2.AlexNet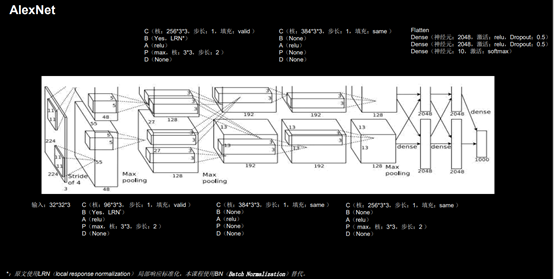
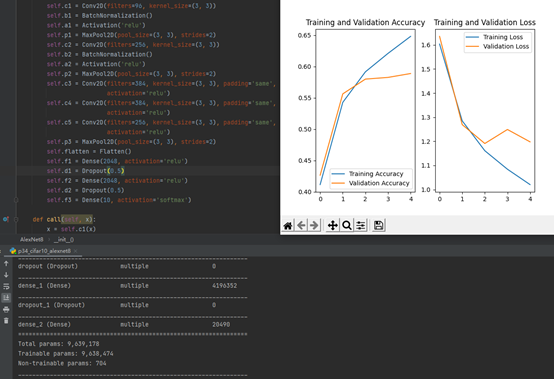
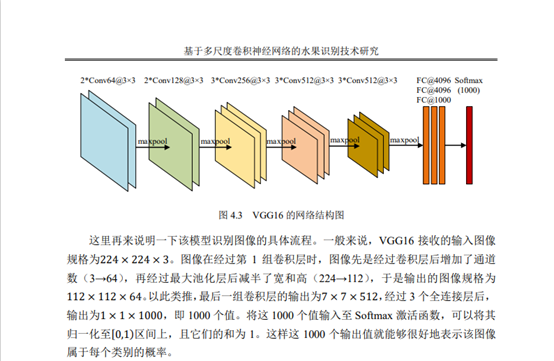
3.VGGNet
4.InceptionNet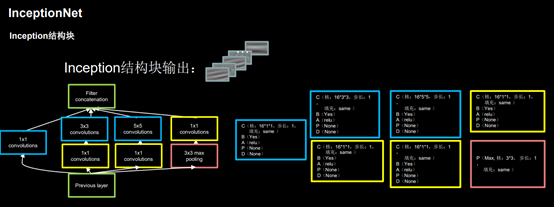
5.ResNet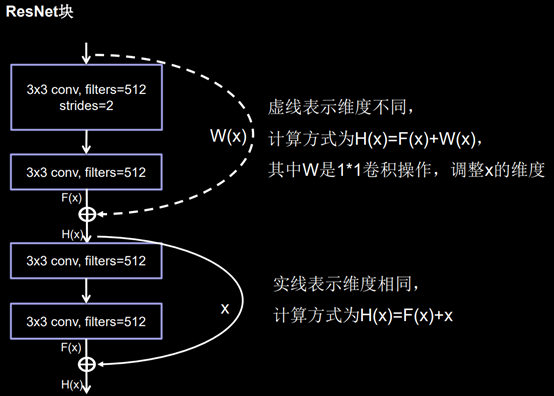
总结: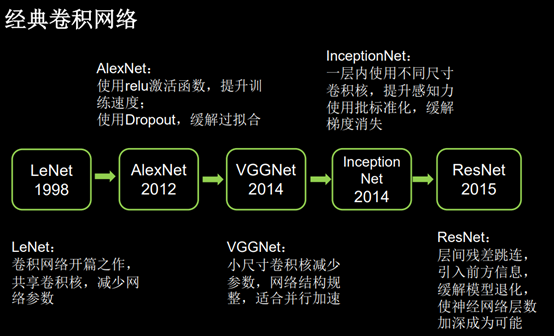
3.阅读论文《基于多尺度卷积神经网络的水果识别技术研究》
遇到的问题和解决办法
无
2021年7月第一周
- 学习了【北京大学】Tensorflow2.0教程 https://www.bilibili.com/video/BV1B7411L7Qt
神经网络优化器: 一言以蔽之,优化器就是在深度学习反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让损失函数(目标函数)值不断逼近全局最小。
五种优化器:
- SGD(随机梯度下降)

- SGDM

- Adagrad

- RMSProp

- Adam

五种优化器训练耗时对比
搭建网络八股sequential


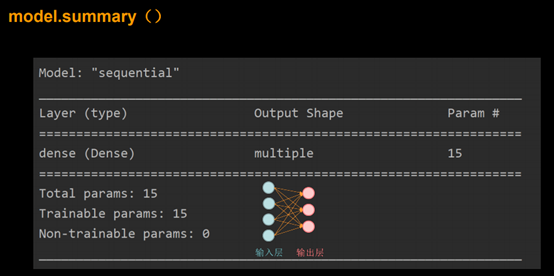
2.完成代码:
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as
plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train =
tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test,
tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db =
tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 =
tf.Variable(tf.random.truncated_normal([4,
3],
stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results =
[] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
# 训练部分
now_time =
time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step,
(x_train, y_train)
in enumerate(train_db):
# batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1)
+ b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
print("Epoch
{}, loss: {}".format(epoch, loss_all
/ 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number
= 0, 0
for x_test,
y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1)
+ b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制
Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()结果: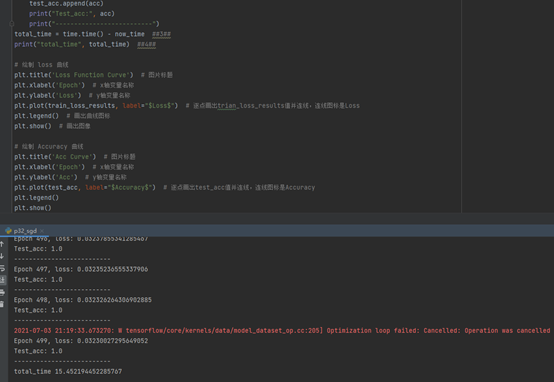
import tensorflow as tf
from sklearn import datasets
import numpy as np
x_train = datasets.load_iris().data
y_train = datasets.load_iris().target
np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
tf.random.set_seed(116)
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(3, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())
])
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
model.fit(x_train, y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20)
model.summary()结果:
2021年6月第四周
- 学习了【北京大学】Tensorflow2.0教程 https://www.bilibili.com/video/BV1B7411L7Qt
损失函数:
均方误差(mean-square error, MSE)是反映估计量与被估计量之间差异程度的一种度量。
交叉熵(Cross Entropy)是Shannon信息论中一个重要概念,主要用于度量两个概率分布间的差异性信息。
欠拟合与过拟合:
欠拟合:模型不能有效拟合数据集,是对现有数据集学习的不够彻底。
过拟合:模型对当前数据拟合的太好,但对从未见过的新数据难以做出正确的判断。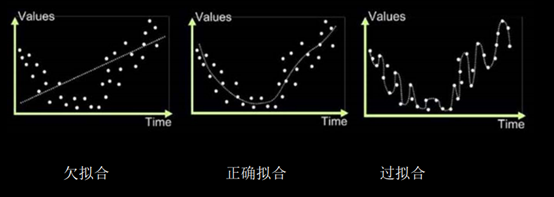
欠拟合的解决方法:
增加输入特征项 增加网络参数 减少正则化参数
过拟合的解决方法:
数据清洗 增大训练集 采用正则化 增大正则化参数
2完成代码:
*"""*
*预测酸奶日销量* *y* *,* *x1* *、* *x2* *是影响日销量的因素。
建模前,应预先采集的数据有:每日* *x1* *、* *x2* *和销量* *y_* *(即已知答案,最佳情况:产量* *=* *销量)
拟造数据集* *X,Y_* *:** y_ = x1 + x2 * *噪声:* *-0.05 ~ +0.05 * *拟合可以预测销量的函数**
"""
* import tensorflow as tf
import numpy as np
SEED = 23455
rdm =
np.random.RandomState(seed=SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + rdm.rand() / 10.0 - 0.05] for (x1, x2) in x]
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 15000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss_mse =
tf.reduce_mean(tf.square(y_ - y))
grads = tape.gradient(loss_mse, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps, w1 is" % (epoch))
print(w1.numpy(),"\n")
print("Final w1 is:", w1.numpy())运行结果:
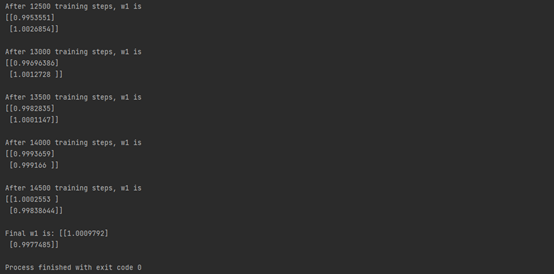
*"""*
*预测酸奶日销量* *y* *,* *x1* *、* *x2* *是影响日销量的因素。
建模前,应预先采集的数据有:每日* *x1* *、* *x2* *和销量* *y_* *(即已知答案,最佳情况:产量* *=* *销量)
拟造数据集* *X,Y_* *:** y_ = x1 + x2 * *噪声:* *-0.05 ~ +0.05 * *拟合可以预测销量的函数**
* *如预测商品销量,预测多了,损失成本;预测少了,损失利润。 若利润 loss tf reduce sum tf select tf greater y y loss mo = . _ . . , _,
_ _, _ _ ( ( ( ) re y y loss less y y ( * *−** * *−** ) ( )))
* *成本,则mse产生的loss无法利益最大化。 如:预测酸奶销量,酸奶成本(COST)1元,酸奶利润(PROFIT)99元。
预测少了损失利润99元,大于预测多了损失成本1元。 预测少了损失大,希望生成的预测函数往多了预测。*
*"""
* import tensorflow as tf
import numpy as np
SEED = 23455
COST = 1
PROFIT = 99
rdm =
np.random.RandomState(seed=SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + rdm.rand() / 10.0 - 0.05] for (x1, x2) in x]
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 15000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
# loss_mse = tf.reduce_mean(tf.square(y_ - y))
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))
grads = tape.gradient(loss, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps, w1 is" % (epoch))
print(w1.numpy(),"\n")
print("Final w1 is:", w1.numpy())运行结果: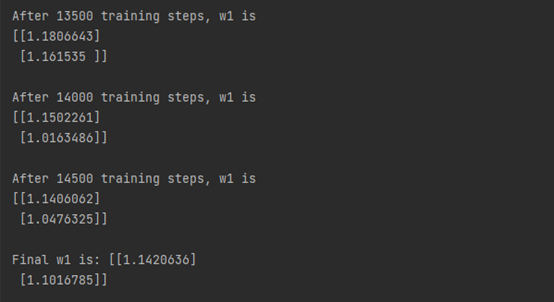
import numpy as np
import tensorflow as tf
import pandas as pd
from matplotlib import pyplot as plt
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])
x_train = np.vstack(x_data).reshape(-1, 2)
y_train = np.vstack(y_data).reshape(-1, 1)
Y_c = [['red' if y else 'blue'] for y in y_train]
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
# 生成神经网络的参数,输入层为2个神经元,隐藏层为11个神经元,1层隐藏层,输出层为一个神经元
w1 =
tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
lr = 0.005
epoch = 800
# 训练部分
for epoch in range(epoch):
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape:
h1 = tf.matmul(x_train, w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 均方误差损失函数
loss = tf.reduce_mean(tf.square(y_train
- y))
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 实现梯度更新
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
if epoch % 20 == 0:
print("epoch:", epoch, "loss:", float(loss))
# 预测部分
print("************predict***************")
# xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx , yy拉直,并合并配对为二维张量,生成二维坐标点
grid =
np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络,进行预测,probs为输出
probs = []
for x_test in grid:
# 使用训练好的参数进行预测
h1 = tf.matmul([x_test], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# y为预测结果
probs.append(y)
# 取第0列给x1,取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs =
np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c)) # squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
# 把坐标xx yy和对应的值probs放入contour<[‘kɑntʊr]>函数,给probs值为0.5的所有点上色 plt点show后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()
轮廓不够平滑存在过拟合现象
添加L2正则化后: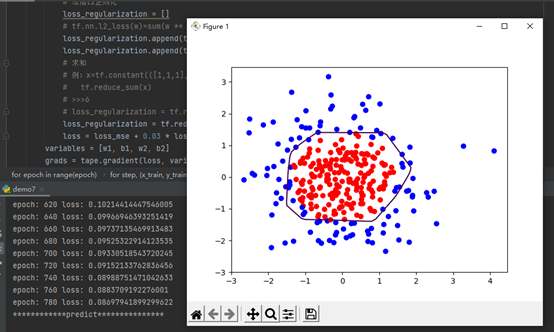
2021年6月第三周
- 学习了【北京大学】Tensorflow2.0教程 https://www.bilibili.com/video/BV1B7411L7Qt
神经网络的复杂度: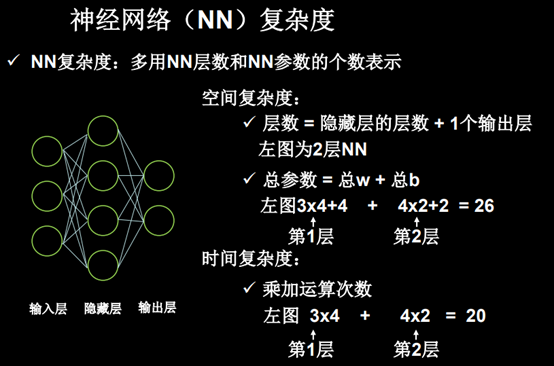
学习率:
指数衰减学习率: 可以先用较大的学习率,快速得到最优解,然后逐步减小学习率,使模型在训练后期稳定。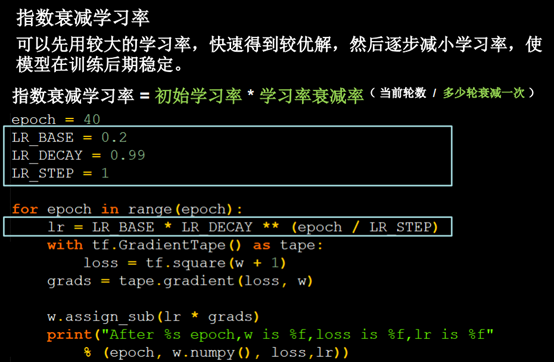
激活函数: 所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
什么是激活函数: 激活函数(Activation functions)对于人工神经网络 1() 模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如图1,在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
为什么使用激活函数: 如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
常用的激活函数: Sigmoid函数、Tanh函数、ReLU函数、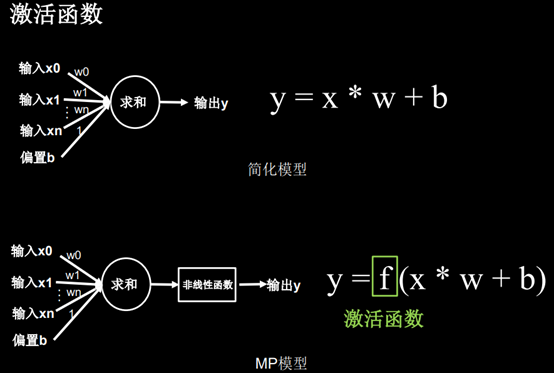

Sigmoid函数: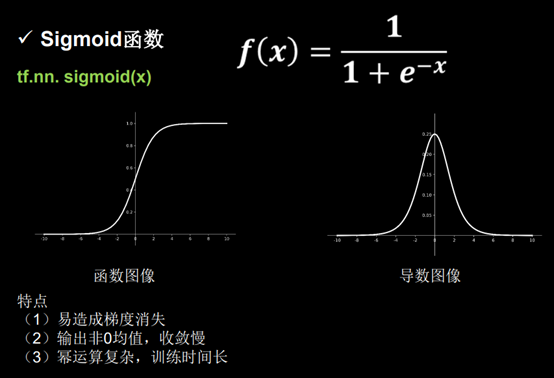
Tanh函数:
ReLU函数:
Leaky Relu函数: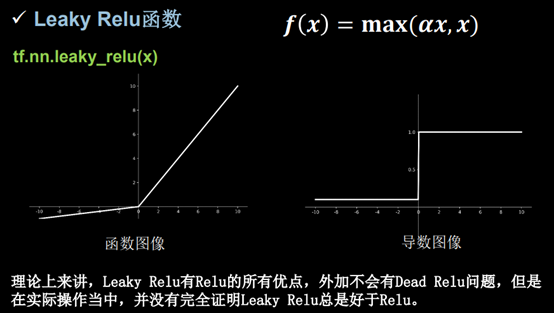

2完成代码:
import tensorflow as tf
import numpy as np
# tf.where()
a =
tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b)
print("c:", c)
#
np.random.RandomState.rand()
rdm =
np.random.RandomState(seed=1)
a = rdm.rand()
b = rdm.rand(2, 3)
print("a:", a)
print("b:", b)
# np.vstack()
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.vstack((a, b))
print("c:\n", c)
# np.mgrid()
x, y = np.mgrid[1:3:1, 2:4:0.5]
grid = np.c_[x.ravel(), y.ravel()]
print("x:", x)
print("y:", y)
print('grid:\n', grid)
# -------------------------------------------------------------------------------------------
# 指数衰减学习率
w =
tf.Variable(tf.constant(5, dtype=tf.float32))
epoch = 40
LR_BASE = 0.2
LR_DECAY = 0.99
LR_STEP = 1
for epoch in range(epoch):
lr = LR_BASE * LR_DECAY ** (epoch /
LR_STEP)
with tf.GradientTape() as tape:
loss = tf.square(w+1)
grads = tape.gradient(loss, w)
w.assign_sub(lr * grads)
print("After %s epoch, w is %f, loss is %f,
lr is %f" %
(epoch, w.numpy(), loss, lr))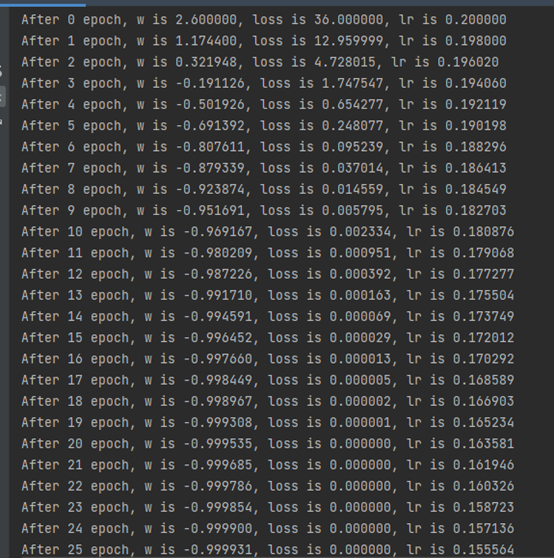
2021年6月第二周
- 学习了【北京大学】Tensorflow2.0教程 https://www.bilibili.com/video/BV1B7411L7Qt








2.编写代码
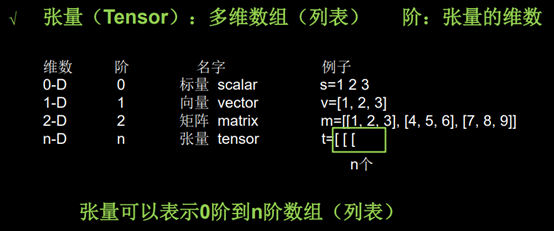
# 创建一个张量
import tensorflow as tf
import numpy as np
a = tf.constant([1, 5], dtype=tf.int64)
print(a)
print(a.dtype)
print(a.shape)
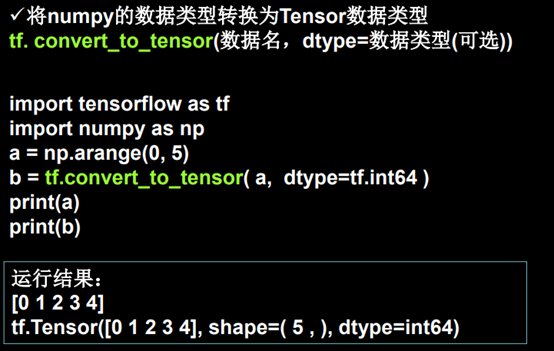
b = np.arange(0, 5)
c = tf.convert_to_tensor(b)
print(c)
d = tf.zeros([2, 3])
e = tf.ones(4)
f = tf.fill([2, 2], 9)
print(d)
print(e)
print(f)
g = tf.random.normal([2, 2], mean=0.5, stddev=1)
print(g)
h = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print(h)
i = tf.random.uniform([2, 2], minval=0, maxval=1)
print(i)
x1 = tf.constant([1, 2, 3], dtype=tf.float64)
print(x1)
x2 = tf.cast(x1, tf.int32)
print(x2)
print(tf.reduce_max(x2), tf.reduce_min(x2))
a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print(a)
print(b)
print(tf.add(a, b))
print(tf.subtract(a, b))
print(tf.multiply(a, b))
print(tf.divide(a, b))3.实验:鸢尾花分类
(1)鸢尾花数据集读入
安装sklearn 和 pandas

读入数据: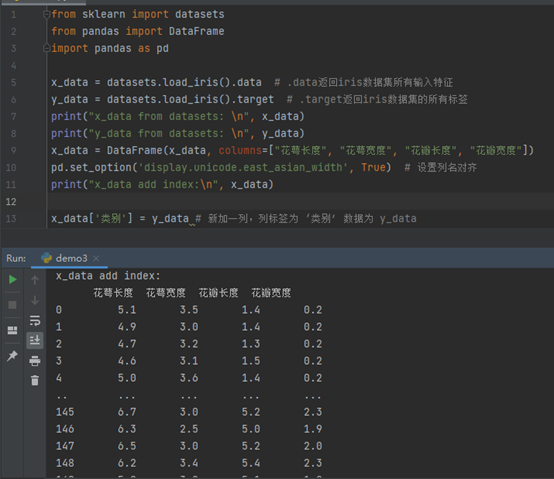
准备数据
• 数据集读入
• 数据集乱序
• 生成训练集和测试集(即 x_train / y_train)
• 配成 (输入特征,标签) 对,每次读入一小撮(batch)
搭建网络
• 定义神经网路中所有可训练参数
参数优化
• 嵌套循环迭代,with结构更新参数,显示当前loss
测试效果
• 计算当前参数前向传播后的准确率,显示当前acc
acc / loss可视化
实验代码:
# -*- coding: UTF-8
-*-
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签
x_data =
datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train =
x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train =
tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
#
from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db =
tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 =
tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results
= [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc =
[] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500
# 循环500轮
loss_all = 0
# 每轮分4个step,loss_all记录四个step生成的4个loss的和
# 训练部分
for epoch in range(epoch):
#数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db):
#batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape:
# with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1
# 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ -
y)) # 采用均方误差损失函数mse =
mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr *
w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all/4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
# 绘制 loss 曲线
plt.title('Loss Function Curve')
# 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()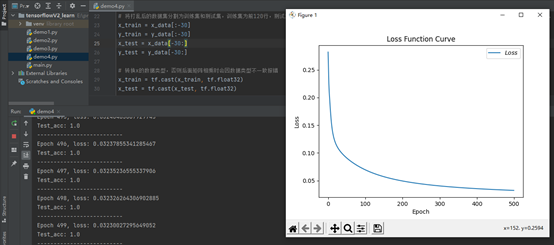
2021年6月第一周
二)本周科研内容、工作进展,遇到的问题等
安装了tensorflow等环境
Pycharm更换pip源为国内
清华大学源:https://pypi.tuna.tsinghua.edu.cn/simple
安装tensorflow2.1
pip install tensorflow -i
https://pypi.tuna.tsinghua.edu.cn/simple --default-timeout=1000
- 学习了【北京大学】Tensorflow2.0教程 https://www.bilibili.com/video/BV1B7411L7Qt
以鸢尾花分类为例:
鸢尾花可分为: 0狗尾草鸢尾 1杂色鸢尾 2佛吉尼亚鸢尾
通过测量花的花萼长、花萼宽、花瓣长、花瓣宽, 可以得出鸢尾花的类别。
神经网络:
- 采集大量(花萼长、花萼宽、花瓣长、花瓣宽,对应的类别(标签,需要人工标定))数据对构成数据集
- 把数据集喂入搭建好的神经网络结构中
- 网络优化参数得到模型
- 模型读入新输入特征,输出识别结果。
如图:


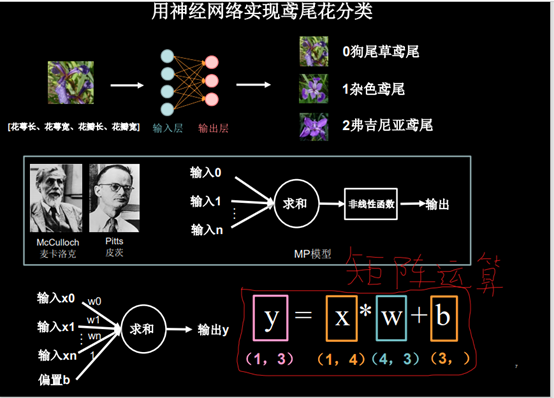
输入 [花萼长、花萼宽、花瓣长、花瓣宽] 1行4列的数据(X)乘 W(权值 4行三列)得到 1行3列的结果。

输入 [花萼长、花萼宽、花瓣长、花瓣宽] 所以有四个输入节点 输出的是三种鸢尾花各自的可能性大小,所以输出节点是3个。
y0,y1,y2 与 前面的x0,x1,x2,x3都有连接关系
称之为全连接网络。
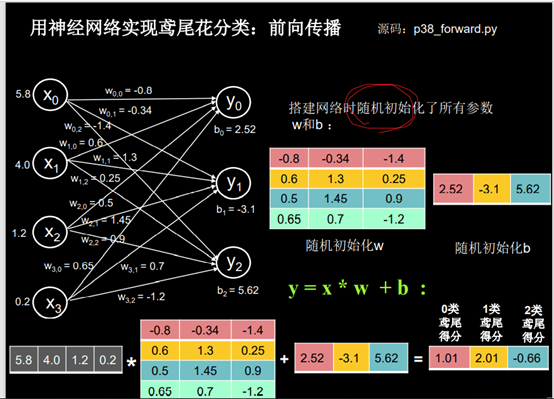




3.编写代码
import tensorflow as tf
# 变量定义
w =
tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40
for epoch in range(epoch):
with tf.GradientTape() as tape:
# with 结构到grads框起了梯度的计算过程
loss = tf.square(w + 1)
grads = tape.gradient(loss, w) # .gradient函数告知谁对谁求导
w.assign_sub(lr * grads) # .assign_sub对变量做自减 即: w -=lr*grads 即 w = w - lr*grads
print("After %s epoch, w is %f,loss is %f" % (epoch, w, loss))
# 最终目的:找到loss最小 即w = -1的最优参数w
随着loss的减小 w趋向-1最终找到了w=-1使loss最小
把学习率改为0.01:
学习率过小时,参数更新缓慢,40次迭代后未能找到最优值
把学习率改为0.999:
学习率过大时,参数在最优值两边跳动,同样没有找到最优值
